Actividades

Actividad 1

Tiempo estimado: 2 h

A partir de la lectura del caso transversal, plantead un posible proyecto de investigación y uno de intervención en EpS.

Actividad 2

Tiempo estimado: 3 h

Planificad objetivos de aprendizaje en un programa de intervención.

Actividad 3

Tiempo estimado: 1 h 30 min.

Identificad cuáles son los modelos teóricos que fundamentan el proyecto elegido en el ejercicio anterior.

Actividad 4

Tiempo estimado: 2 h

Realizad una búsqueda bibliográfica en el Catálogo colectivo de Cataluña del Consorcio de Bibliotecas de Cataluña (http:\\www.cbuc.es) de cinco libros útiles para el proyecto elegido anteriormente y recoged de cada uno la información bibliográfica (localización, autor, título, publicación, descripción física, colección, nota, materia, descriptores, entrada e ISBN).

Actividad 5

Tiempo estimado: 2 h

Identificad y justificad cuál sería el mejor diseño que se debería plantear para el proyecto elegido.

Actividad 6

Realización de una tabla de frecuencias

Tiempo estimado: 30 min.

En un estudio sobre el nivel de azúcar en la sangre hemos obtenido los siguientes resultados:

Tabla 1

Hipo = nivel de glucosa inferior al normal

Iso = nivel de glucosa normal

Hiper= nivel de glucosa superior al normal

1. Realizad una tabla de frecuencias de los datos recogidos con todas las frecuencias posibles.

En un estudio sobre la presión arterial en pacientes de diálisis hemos obtenido los siguientes valores:

Tabla 2

2. Realizad una tabla de frecuencias de los datos recogidos.

b1. ¿Cuántos intervalos tendrá la tabla? ¿Cómo se determina habitualmente?

b2. ¿Qué anchura tendrá cada intervalo? ¿Cómo lo habéis calculado?

b3. ¿Es una tabla de una o de doble entrada? ¿Por qué?

Es muy importante indicar toda la información necesaria tanto en la tabla de frecuencias, como en el gráfico (títulos, unidades, variables, etc.).

Actividad 7

Realización de gráficos

Tiempo estimado: 30 min.

Utilizad las herramientas informáticas a vuestro alcance para realizar las siguientes representaciones gráficas:

1. Representad gráficamente los datos de la tabla 1.
2. Representad gráficamente los datos de la tabla 2.

Podéis utilizar diferentes tipos de gráficos para cada tabla.

Recordad que podéis utilizar los gráficos de la hoja de cálculo EXCEL del OFFICE de Microsoft.

Actividad 8

Cálculo de los estimadores de tendencia central

Tiempo estimado: 30 min.

1. Calculad todos los estimadores de tendencia central de la tabla 1.
2. Calculad la mediana, la moda y la media aritmética de los datos de la tabla 2.
3. Escribid una posible explicación al hecho de que determinadas variables humanas sean bimodales e indicad algún ejemplo.
4. ¿Puede darse el caso de que, obteniendo los mismos valores de la mediana, moda y media aritmética, dos muestras sean diferentes y, por lo tanto, también las poblaciones? ¿Por qué sucede esto? Proponed un ejemplo y razonadlo.

Para realizar los cálculos podéis utilizar una hoja de cálculo (por ejemplo, Excel), la calculadora científica o los cálculos sobre el papel.

Actividad 9

Cálculo de los estimadores de dispersión o variabilidad

Tiempo estimado: 1 h

1. Calculad la amplitud, variancia, desviación típica y coeficiente de variación de los datos de la tabla 2.
2. Analizando los dos gráficos siguientes (gráfico 1 y gráfico 2), ¿en qué caso la desviación típica es mayor? Razonad la respuesta.

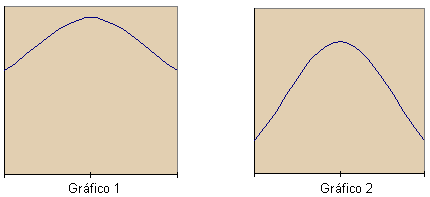
3. ¿Qué repercusiones estadísticas se derivan del caso de una variable que presenta una desviación típica muy alta? ¿En qué caso resulta más probable acertar las conclusiones finales, cuando la desviación típica de la variable es alta o cuando es baja? Razonad la respuesta.
4. ¿Qué sentido aporta el coeficiente de variación de Pearson? ¿Podemos saber si la variación de dos variables en una población es más o menos de la misma magnitud? Justificad la respuesta.
5. Hemos realizado un estudio entre los practicantes de un determinado deporte y hemos obtenido los estimadores de la tabla 3. ¿Podemos afirmar que la variable peso manifesta el mismo nivel de variabilidad que la variable altura? Razonad la repuesta mediante cálculos.

Tabla 3

Actividad 10

Cálculo del intervalo de confianza y dimensión de una muestra en una variable cuantitativa

Tiempo estimado: 30 min.

Actividad 11

Cálculo del intervalo de confianza y medida de una variable cuantitativa

Tiempo estimado: 30 min.

Queremos conocer la frecuencia de fumadores entre las personas con problemas de depresión. En la bibliografía consultada tenemos como referencia que, en otro estudio realizado, la frecuencia de fumadores entre las personas con depresión era del 45%.

Actividad 12

Cálculo de las dimensiones de una muestra en un test de hipótesis

Tiempo estimado: 30 min.

Pretendemos realizar un estudio experimental sobre un nuevo fármaco para el tratamiento de la migraña. Queremos valorar si el nuevo tratamiento presenta unos resultados más satisfactorios que el tratamiento habitual utilizado. Los parámetros que proponemos para el estudio son: el riesgo de error alfa es del 5% y el riesgo de error beta es del 10%. El nivel de confianza que se exige es del 90%. Se han realizado unas experiencias previas en las que se ha detectado que el nivel de mejora con el tratamiento estándar es del 40%, mientras que con el nuevo tratamiento es del 50%.

1. Indicad en este caso cuáles son las hipótesis nula y alternativa del experimento.
2. Indicad cuáles son los errores alfa y beta del experimento.
3. Calculad el número mínimo que deben tener las muestras según el planteamiento expresado en el enunciado.

Actividad 13

Las funciones de distribución

Tiempo estimado: 30 min.

1. Intentad explicar en pocas palabras por qué la estadística utiliza conceptos de probabilidad.
2. ¿Cuál de los gráficos 3 y 4 pertenece a una función de distribución de una variable cuantitativa? Razonad la respuesta. 

3. Muchas variables biológicas siguen la función de distribución normal. Explicad las características básicas de esta función.
4. ¿En qué consiste la distribución normal reducida y qué sentido estadístico presenta?