Tal como ya se ha comentado en el módulo 3 (Metodología II: elaboración de un proyecto de investigación) hay que tener en cuenta diferentes consideraciones referentes a la utilización de la mediana y de la media como parámetros de centralización.

Observad las tablas de frecuencias de dos variables que denominaremos ejemplo1 y ejemplo2 donde hay dos muestras que presentan mediana y media idénticas.

Ejemplo 1

Intervalos	PMI	ni	Fi	Ni	Fi
[0,5-1,5]	1	5	0,10	5	0,10
[1,5-2,5]	2	8	0,16	13	0,26
[2,5-3,5]	3	16	0,32	29	0,58
[3,5-4,5]	4	17	0,16	46	0,92
[4,5-5,5]	5	4	0,08	50	1,00
		50

Ejemplo 2

Intervalos	PMI	ni	Fi	Ni	Fi
[0,5-1,5]	1	5	0,10	5	0,10
[1,5-2,5]	2	17	0,34	22	0,44
[2,5-3,5]	3	16	0,32	38	0,76
[3,5-4,5]	4	8	0,16	46	0,92
[4,5-5,5]	5	4	0,08	50	1,00
		50

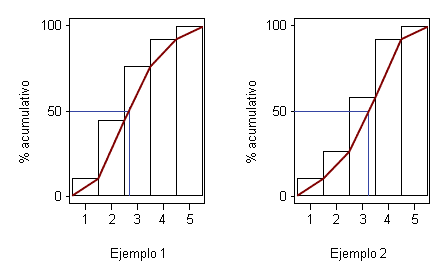
Ambos ejemplos corresponden a conjuntos de cincuenta datos; en ambos casos, la "clase medianera" será la que tiene como marca de clase 3.0 (donde la frecuencia relativa acumulada supera el 50%), pero los polígonos de frecuencias relativas son muy diferentes.

Si imaginamos los cincuenta datos de cada conjunto distribuidos y ordenados de esta manera se ve claramente que, aunque los valores centrales de una distribución y de otra están en la clase del 3.0, en el primer caso quedan "al principio" de la clase y en el segundo caso "al final". Esta idea nos sugiere la conveniencia de ajustar más el valor de la mediana.

Recordad que la mediana es el valor de la distribución por la que la frecuencia relativa acumulada es del 50%.

Para materializar la observación de la mediana como valor al que le corresponde la frecuencia acumulada del 50% se han trazado las líneas en verde sobre los gráficos anteriores:

• Se dibuja a la altura del 50% del eje una recta paralela al eje de abcisas, hasta que corte la poligonal.
• A partir de este punto de corte se traza una recta paralela en el eje de ordenadas para leer la abcisa correspondiente a aquel punto de corte.
• El valor determinado sobre el eje es la mediana.

La mediana del primer conjunto de datos sobre el gráfico es, aproximadamente, 2.7, y la del segundo conjunto de datos, 3.2.

Recordad que el ejemplo que se acaba de realizar sigue una idea conceptual ("teórica") asociada a la tabulación de una variable continua medianera, se puede establecer una fórmula para el cálculo de la mediana como variable continua, que se puede escribir aquí:

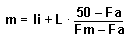                  [0].

Si se aplica esta fórmula, naturalmente más precisa que la observación de los gráficos, en los dos ejemplos anteriores, las medianas resultantes son 2,69 y 3,25.

Puesto que la asignación de rangos corresponde a la idea de ordenar los datos de una variable, se tienen en cuenta estas ideas para el cálculo de los cuartiles de una distribución de N datos:

• Si N es impar, hay un dato central, que es la mediana, que corresponde al valor del dato que tiene rango (N+1)/2 (este rango será un número entero).
• Si N es par , (N+1)/2 no será entero; la mediana se obtiene en este caso sumando y dividiendo por dos los datos que corresponden a los dos enteros entre los cuales está comprendido el rango (N+1)/2.
• El primer cuartil es el dato que corresponde al rango (N+1)/4 (si este rango es un número entero). Si (N+1)/4 no es entero, el primer cuartil se obtiene interpolando adecuadamente entre dos los datos que tienen como rangos los dos enteros entre los cuales está comprendido (N+1)/4.
• Para el tercer cuartil se actúa igual que en el primer cuartil, pero con el rango 3(N+1)/4.

En el caso de las variables continuas se puede realizar para los cuartiles un tratamiento conceptual parecido al de la mediana:

• El primer cuartil corresponde al valor que tiene como frecuencia relativa acumulada, leída sobre el polígono de frecuencias acumuladas, el 25%.
• El tercer cuartil corresponde al valor que tiene como frecuencia relativa acumulada, leída sobre el polígono de frecuencias acumuladas, el 75%.

Se puede establecer también una fórmula, derivada de la aplicación de la semblanza de triángulos, para cada cuartil. Lo primero que hay que hacer, en el caso de tener únicamente una tabulación de datos de una variable continua, será localizar las clases a las que pertenecen los cuartiles. Seguidamente, una fórmula como la que se ha dado para la mediana pero sustituyendo el cincuenta por veinticinco en el caso del primer cuartil y por setenta y cinco en el caso del tercero nos dará los valores más precisos para estos cuartiles.