La búsqueda de un modelo para describir las relaciones entre variables empieza con las funciones de manipulación más sencillas: las funciones lineales.

Cuando se está convencido de la bondad de un estudio de nube de puntos de una distribución bivariante mediante la línea recta, primero intuitivamente sobre el gráfico y posteriormente con el cálculo del coeficiente de correlación, conviene saber la manera adecuada de dibujar la recta que mejor describa la relación entre las variables. Esta recta recibe el nombre de recta de regresión.

La primera posibilidad intuitiva para dibujar la recta puede ser hacerlo a ojo, intentando entender cuál es la recta que mejor se adapta a la nube de puntos. Pero es mejor utilizar un programa informático.

Cuando se quiere obtener la fórmula de la recta de regresión se utiliza el método de los mínimos cuadrados. Se trata de razonar cuáles deben ser los valores de los coeficientes a y b que hacen que la suma de los cuadrados de los residuos de las observaciones reales, respecto del modelo de ajuste dado por la función y = a + b·x tenga el valor mínimo posible.

Se puede demostrar lo siguiente:

• Que la pendiente de la recta de regresión y = a + bx es:

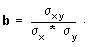
La recta de regresión, y = a + bx, que pasa por el punto medio de la distribución será:

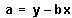
La recta calculada se denomina recta de regresión de y sobre x porque parte de una variable de entrada, o predictora, que supone que está en mayor medida bajo control del experimentador.

Una vez establecido el modelo, en este caso lo que nos da la recta de regresión, podremos hacer predicciones del valor que puede tener la variable de respuesta: el valor nos da la función "modelo", para cierto valor x₀, es decir, lo que hemos definido como ajuste, será el valor que estimaremos.

Puesto que el coeficiente de correlación mide cuán estricto es "el acercamiento de la nube de puntos a una línea recta", es intuitivo que cuanto más grande sea el valor absoluto de coeficiente, más fiabilidad tendrán las predicciones que se puedan hacer y más pequeño será el margen de error con que se deberán enunciar.

Se deberán recoger las notas del grupo de alumnos objeto de estudio. Nos dan las tablas siguientes, recogidas en un conjunto de 339 alumnos:

No se podría decir, de ninguna manera, que queremos hacer una estadística bivariante, lo único que podríamos hacer es una descripción global de cada variable.

Con las tablas anteriores no podríamos relacionar las variables; para hacerlo necesitaríamos saber, por ejemplo, si los alumnos que han obtenido "buenas notas" de catalán corresponden, en buena parte, a los que han obtenido los excelentes de castellano, o no; si el conjunto de insuficientes en una materia y la otra tiene una intersección muy gande o no; y todo esto no se puede deducir de las tablas anteriores.

A continuación, empezamos el estudio práctico de presentación de datos de la estadística bivariante.

Veamos una tabla cruzada que se corresponde con las tablas anteriores:

En una tabla cruzada se incluye siempre una fila y una columna de totales; estas distribuciones de totales reciben el nombre distribuciones marginales.

A partir de los datos se pueden construir las distribuciones marginales, pero no al revés.

Ahora ya se pueden contestar las preguntas que nos formulábamos antes. Ya podemos estudiar las relaciones entre las dos variables.

Para analizar el comportamiento conjunto de las dos variables interesa constatar si hay asociación de valores, es decir, si se puede observar que algún(os) valor(es) de una variable tienden a aparecer aparejados con algún(os) valor(es) de la otra variable.

Para poder realizar más detalladamente el análisis de una tabla cruzada, a veces se presentan los datos no con frecuencias absolutas, sino con porcentajes respecto del total de datos.

En otras ocasiones, interesa analizar el comportamiento de una variable para cada valor concreto de la otra, y entonces se presenta una tabla donde se han calculado los porcentajes por filas (que nos dan los perfiles fila de la distribución) o bien los porcentajes por columnas (y entonces aparecen los perfiles de columna).