El camino intuitivo para realizar un cálculo que permita valorar el grado de ajuste (o de desajuste) entre las frecuencias observadas (empíricas) y las frecuencias esperadas (teóricas) es el siguiente:

• Calcular las diferencias entre unas frecuencias y otras para poder medir la discrepancia que hay entre sí.
• Positivar esta diferencia, porque tanto se aparta del modelo una diferencia en un sentido como en otro. Las elevaremos al cuadrado tal como se realiza la desviación estándar, por ejemplo. Si no lo hicieramos así, unas desviaciones se compensarían con otras en lugar de sumarse.
• Relativizar o ponderar las diferencias cuadráticas obtendias. No es lo mismo obtener 22 flores rosas más de la cuenta en un cruce que ha dado 444 flores, que obtener 22 en un cruce que ha dado 4.444 flores. Esta relativización se realiza tomando como referencia los valores esperados.
• Sumar para obtener la discrepancia total.

Matematizando el itinerario sugerido obtenemos lo siguiente:

• Si O_y representa la frecuencia observada en cada clase, E_y la frecuencia esperada en aquella clase de acuerdo con el modelo teórico que queremos confrontar, se define un estadístico que se representa como X² mediante un sumatorio que se extiende a todas las clases de valores observados.

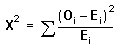
Conviene que observéis que no todos los valores de las diferencias O_y–E_y son independientes uno de otro, sino que su suma es 0. Si hay n clases de valores, sólo n–1 de las diferencias mencionadas son independientes.

Por ejemplo, si hemos observado 22 flores rosas "de más" respecto a las esperadas, seguro que habríamos obtenido menos flores blancas y menos flores rojas de las esperadas, 22 en total.

Suponiendo que la hipótesis nula es correcta, es decir que el modelo dado por las frecuencias esperadas se adecua con la experiencia que estudiamos, entonces el estadístico X² tiene un modelo teórico prefectamente conocido: si hay n clases de valores es la distribución ji cuadrado con n–1 grados de libertad, representada como c ².

• Conviene que conozcáis cómo se escribe la letra griega ji (también designada como qui o ji): y que sepáis que la mayúscula X se reserva para el estadístico y la minúscula c para representar la distribución de probabilidad.
• La distribución ji cuadrado con k grados de libertad se presenta habitualmente como suma de cuadrados de k distribuciones normales estándares. Puesto que se puede demostrar que para cada clase (O-E)²/E se distribuye como una normal estándar y puesto que sólo hay n-1 de estas observaciones independientes, el modelo para el estadístico X² es la distribución ji cuadrado con n–1 grados de libertad.

Hay dos formas de confrontar el estadístico X² obtenido con la distribución ji cuadrado que da el modelo teórico del estadístico.

• Establecer una región crítica que indicará cuáles son los valores del estadístico X² que nos harán rechazar la hipótesis nula. Éste sería el procedimiento utilizado en el trabajo "manual", que podemos realizar mediante la consulta de tablas publicadas en los manuales de estadística.

Considerar el denominado p-valor del valor de X² observado.

El punto de vista que ahora comentamos es el más utilizado en el trabajo con el ordenador. Necesitaremos comparar el p-valor correspondiente a nuestros datos (ésta es la información que nos proporciona el ordenador) con el riesgo máximo que queremos aceptar (que está prefijado y que, recordadlo, se denomina nivel de significación de la prueba) para decidir si debemos mantener como válida la hipótesis nula o bien tenemos criterios para rechazarla.