|
Cálculos de las medidas de tendencia central |
| ||
 Media aritmética
Media aritmética
La media o promedio es la suma de las mediciones observadas dividida por el número de observaciones. La fórmula y notación científica para el cálculo de la media de los datos individuales es:
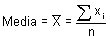
Esta fórmula se lee como "x-barra" y equivale a la suma de los x’s dividida por el total de observaciones n.
Por ejemplo, en un brote de hepatitis A, 6 personas enfermaron con síntomas de 24 a 31 días después de la exposición. Los periodos de incubación para las personas afectadas fueron 29, 31, 24, 29, 30 y 25 días. Para calcular el periodo de incubación promedio de este brote, deberemos sumar las observaciones individuales y luego dividirlas por el número total de observaciones de la manera siguiente:

- sumar las observaciones: 29 + 31+ 24 + 29 + 30 + 25 = 168
- contar el número de observaciones: 6
- resultado: 168/6 = 28 días
 Mediana
Mediana
La mediana es el nivel de medición por debajo y por encima del cual se ubican la mitad de las observaciones; es también el 50º percentil. La mediana es particularmente útil para representar la ubicación central cuando se inclinan los datos. Para calcular la mediana, el grupo de datos se debe poner en primer lugar en el orden de rango de menor a mayor, o viceversa. Por ejemplo, suponed que vosotros habéis medido la presión arterial sistólica (en mm/Hg) de un grupo de cinco pacientes. Los resultados fueron 110, 120, 122, 130 y 180. En este ejemplo, dos observaciones son mayores que 122, y dos son menores; por lo tanto, la mediana es 122 mm/Hg, el valor de la tercera observación. Notad que el promedio (mm/Hg de 132) es mayor que el 4º de los cinco valores.
¿Cómo identificar la mediana de unos datos?
- Organizad las observaciones en orden ascendente o descendente.
- Encontrad el rango medio con la fórmula siguiente:
 .
.- Si el número de observaciones (n) es impar, el rango medio cae en una observación.
- Si n es par, el rango medio cae entre dos observaciones.
- Identificad el valor de la mediana:
- Si el rango medio cae en una observación específica (es decir, si n es impar), la mediana es igual al valor de esta observación.
- Si el rango medio cae entre dos observaciones (es decir, si n es par), la mediana es igual al promedio (es decir, a la media aritmética) de los valores de estas observaciones.

Ejemplo con un número impar de observaciones.
Ejemplo con un número par de observaciones.
 Moda
Moda
La moda es la observación que ocurre más comúnmente en una distribución de frecuencias. Para encontrar la moda, deberéis construir una distribución de frecuencias en la que tabuléis con qué frecuencia ocurren los valores. Por ejemplo, los siguientes son datos sobre la paridad ordenados de manera ascendente:
0, 0, 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 6.

Ya que 1 ocurre 4 veces, más que cualquier otro valor, podemos determinar que la moda es 1. Si, en otras situaciones, cada valor ocurre sólo una vez, la distribución no tiene ninguna moda. Además, si dos o más valores se unen como el más común en la misma situación, la distribución tiene más de una moda.

