|
Cálculos para medidas de dispersión |
| ||
Contamos con otros índices estadísticos de frecuencia que también son importantes para describir la cantidad de variación que está presente en un grupo de mediciones.
 Rango
Rango

La medida más sencilla de dispersión es el rango, que es la diferencia entre la observación más alta y la más baja. Esta medida puede expresarse como "desde (el mínimo) hasta (el máximo)", que son dos números en la distribución de frecuencias. Tal como podemos ver, esta medida es muy sensible a los valores extremos en cualquier dirección, o en ambas.
 Cuartiles y percentiles
Cuartiles y percentiles
Otras medidas de dispersión usadas comúnmente en una distribución de frecuencias son los cuartiles y los percentiles.
Los cuartiles de una distribución de frecuencias dividen la distribución en 4 partes iguales. Para obtener la posición de los cuartiles, los datos se organizan en orden ascendente; luego se dividen en 4 grupos, cada uno de ellos contendrá un 25%. Así fue como se calculó el valor de la mediana, si el grupo contiene un número par de observaciones, entonces el valor de los cuartiles se ubica entre el valor de aquellas observaciones intermedias, o sea, el cuartil es el promedio de aquellas observaciones. Examinad, por ejemplo, las siguientes series de 20 valores:
|
3, 3, 4, 4, 5; |
6, 6, 6, 7, 7; |
7, 8, 9, 9, 10; |
10, 11, 11, 12, 13. |
El primer cuartil corresponde al valor de las 5as y 6as observaciones (5,5); el segundo cuartil corresponde a la mediana (7); el tercer cuartil es el valor entre las 15as y las 16as observaciones (10); y el cuarto cuartil corresponde al valor máximo (13).
También podemos considerar el valor máximo de una distribución de otra manera. Podéis pensar en éste como un valor en un grupo de datos que tiene un 100% de las observaciones en –o debajo de– éste. Cuando se considera de esta forma, se denomina 100 o centésimo percentil. Desde esta perspectiva, la mediana es el 50º percentil. Los percentiles más comúnmente usados, diferentes de los promedios, son los 25os y los 75os percentiles, que también demarcan el primer y tercer cuartiles.
 Varianza y desviación estándar
Varianza y desviación estándar
La varianza y la desviación estándar son otras medidas útiles, las más usadas para expresar la dispersión de un grupo de datos. Éstas consideran, no sólo la dispersión en sí, sino también de qué manera tiene lugar la dispersión alrededor del valor medio o de la ubicación central de la distribución. Si restáis la media de cada observación, la suma de las diferencias será 0. Este concepto de restar la media es la base de estas otras dos medidas de dispersión. Un primer paso para estas medidas es elevar al cuadrado cada diferencia para eliminar los números negativos, a continuación, se suman las diferencias al cuadrado y, finalmente, se dividen por el número de observaciones menos 1 para encontrar un "promedio" de la diferencia al cuadrado. Este promedio es la varianza. Para convertir posteriormente la varianza en las unidades originales, tomaremos la raíz cuadrada. La raíz cuadrada de la varianza se llama desviación estándar. Debido a sus propiedades matemáticas, la desviación estándar es mucho más útil como índice de la variación. La desviación estándar es una medida de la distancia promedio de la observación de su media.
Fórmulas para calcular la varianza y la desviación estándar desde datos individuales
Podéis utilizar las fórmulas que os damos a continuación para calcular la varianza y la desviación estándar, pero esto sería problemático si el grupo de datos fuese muy grande. Las fórmulas siguientes son las más utilizadas para calcular estas medidas, ya que no requieren calcular inicialmente la media. A continuación, tenemos las fórmulas computacionales:
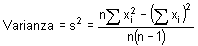
 .
.
Comparad los dos términos  y
y 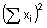 . El primero indica que eleváis al cuadrado cada observación y que luego sumáis los valores al cuadrado. El segundo término indica que encontráis la suma de las observaciones y que luego eleváis la suma al cuadrado.
. El primero indica que eleváis al cuadrado cada observación y que luego sumáis los valores al cuadrado. El segundo término indica que encontráis la suma de las observaciones y que luego eleváis la suma al cuadrado.

Mostraremos ejemplos de cómo utilizar ambos grupos de fórmulas, así como la definición de las fórmulas y su parte computacional.
 La curva de distribución normal y el rango normal
La curva de distribución normal y el rango normal
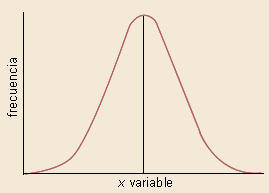
La curva normal (o Gaussiana) es un modelo teórico adecuado para la descripción de muchos fenómenos que ocurren naturalmente. Para usar el modelo, necesitamos tener conocimiento de la media y de la desviación estándar, denotadas por
m y s, respectivamente. Esta curva tiene forma de campana, es simétrica alrededor de la media, con un 95%, aproximadamente, de su frecuencia relativa en el intervalo de m +/ - 2s . Para ilustrar la relación entre la media y la desviación estándar, considerad la siguiente figura:
|
|
Distribución normal o curva de Gauss |
Se muestran los datos distribuidos normalmente. Podéis observar que un 68,3% del área bajo la curva se encuentra entre la media y +/ - 1 desviación estándar. Además, el 95,5% del área se encuentra entre la media y +/ - 2 desviaciones estándares, y un 99,7% del área, entre la media y +/ - 3 desviaciones estándar.

En Biología es una práctica común tomar como límites normales entre los 2,5.os y 97,5.os percentiles de una distribución de las mediciones de una población, o sea, el área bajo la curva que contendría un 95,5% de los valores observados.