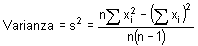Ejemplo

Utilizaremos las fórmulas computacionales para calcular la varianza y la desviación estándar de los datos que hemos usado en el último ejemplo:

Fórmulas:

; .

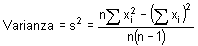Xi

Xi 2

0
1
2
3
4
5
6
7
8
9
10

0
1
4
9
16
25
36
49
64
81
100

Total

55

385

  1. Calculad el término S xi2 en la fórmula, elevad cada observación al cuadrado y encontrad la suma de los cuadrados (observad la segunda columna xi2 de la tabla anterior).

    2. S xi2 = 385

    S : letra griega sigma : sumatoria de
    n o N: el número de observaciones
    fi :     frecuencia de xi
    xi:     i-th observación (x1: primera observación, x4: cuarta observación)

  2. Calculad el término (S xi)2 en la fórmula, encontrad la suma de las observaciones y elevadla al cuadrado (observad la primera columna xi).

    (S xi)2 = 552 = 3.025

  3. Calculad el numerador:

    nS xi2 - (S xi)2 = (11)(385) - 3025= 4.235 - 3.025 = 1.210

  4. Calculad el denominador restando 1 de n y multiplicando el valor por n:

    n (n - 1) = 11(10) = 110

  5. Finalizad calculando la varianza al dividir el denominador entre el numerador:

    s2 = 1.210 / 110 = 11,00

  6. Encontrad la desviación estándar tomando la raíz cuadrada de la varianza:

    s = Ös2= Ö 11,00 = 3,317 = 3,3

Arriba
Cerrar