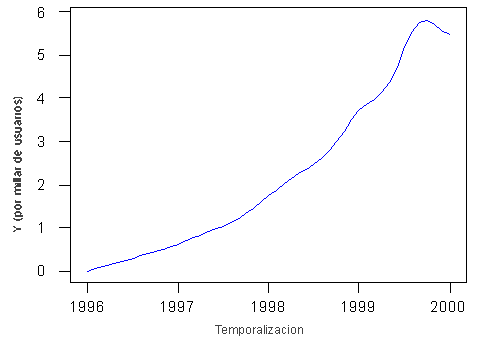
Suponed que queremos estudiar la evolución de una determinada variable (por ejemplo, del valor de un determinado fondo de inversión) a lo largo del tiempo. Este valor, que vamos observando a medida que pasan los días, constituye un ejemplo de la llamada serie temporal. El estudio de las series temporales es básico en el ámbito económico y empresarial, dado que a la hora de hacer previsiones o de crear expectativas futuras se constituye en el método cuantitativo más utilizado.

La recta de regresión que se calcula de una serie temporal, en la que la variable tiempo es la variable independiente, nos marca cuál es la tendencia de la serie. Esta tendencia es uno de los cuatro componentes en que se puede descomponer una serie temporal. Las otras tres son el ciclo, el componente estacional y el componente errático.

El coeficiente de correlación para las series temporales se denomina correlación serial. Ya sabemos cómo calcular esta correlación para dos variables mediante la fórmula de Pearson; pues para calcular la correlación serial tenemos que calcular la correlación de una variable sobre sí misma. Lo que se busca encontrar con la correlación serial es, por ejemplo, qué relación se establece entre el valor de un determinado periodo con el valor que tiene en el periodo inmediatamente siguiente.