Regresión lineal simple
E N U N C I A D O :
Suponed que una muestra aleatoria de siete familias tenía los siguientes ingresos y ahorros anuales:
|
Familia |
Ingresos X |
Ahorros Y |
|
A |
3,6 |
250 |
|
B |
2,5 |
210 |
|
C |
7,8 |
800 |
|
D |
5,6 |
500 |
|
E |
5,3 |
510 |
|
F |
3,3 |
300 |
|
G |
6,1 |
650 |
Ahora responderemos a las siguientes cuestiones utilizando Minitab:
Apartado 1. Representad la nube de puntos.
Apartado 2. Calculad la recta de regresión. Según esta recta de regresión, ¿qué ahorros podemos estimar que tendrá una familia que tiene unos ingresos de 4,8 millones de pesetas?
Apartado 3. Dibujad la recta de regresión.
Apartado 4. Encontrad el error estándar de la pendiente y el intervalo de confianza del 95%.
Apartado 5. ¿Es significativa la influencia de la variable ingresos, X, en la evolución de los ahorros de las familias Y (es decir, la pendiente es significativamente diferente de cero)?
Apartado 6. Indicad cuál es la bondad de ajuste (o también, la varianza explicada por la recta de regresión).
S O L U C I Ó N :
Apartado 1:
En primer lugar, ejecutad el programa Minitab con los datos del caso práctico  .
.
Para dibujar la nube de puntos tenéis que hacer lo siguiente:
 | Haced Graph / Plot. |
 | Introducid la variable independiente (X) y la variable dependiente (Y) en la columna que corresponda. |
 | Al hacer OK obtendréis el siguiente resultado: |
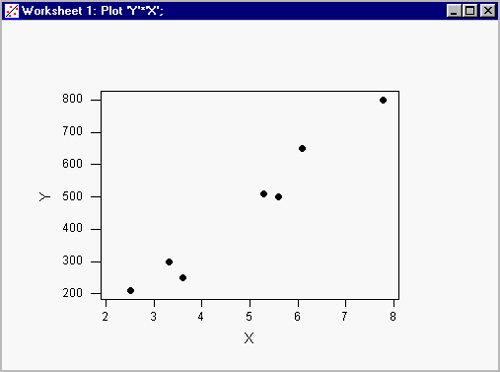
A partir de esta representación, y como una primera aproximación, se puede observar que las dos variables parecen seguir una relación lineal. Por tanto, parece natural intentar calcular cuál es la recta de regresión que explicita esta relación lineal.
Apartado 2:
En primer lugar, ejecutad el programa Minitab con los datos del caso práctico .
.
Para calcular la recta de regresión, tenéis que hacer:
 | Stat / Regression / Regression. |
 | Introducid la variable dependiente Y, Response, y la variable independiente X, Predictors. |

La recta de regresión es Y = –110 + 117 X. Ahora, si queremos estimar el ahorro de una familia que tiene unos ingresos anuales de 4,8 millones de pesetas, sólo hay que sustituir la variable X para este valor y obtener la Y:
Y = -110 + 117 · 4,8 = 451,6
Por tanto, según la recta de regresión encontrada, se prevé que la familia ahorrará unas 451.600 pesetas.
Apartado 3:
En primer lugar, ejecutad el programa Minitab con los datos del caso práctico  .
.
Con la representación de la recta de regresión encima de la nube de puntos, se puede ver la relación lineal que se establece entre ambas variables.
 | Haced Stat / Regression / Fitted Line Plot. |
 | Introducid la variable dependiente Y, Response, y la variable independiente X, Predictor. Marcad la opción Linear. |
 | El gráfico que obtendréis es el siguiente: |
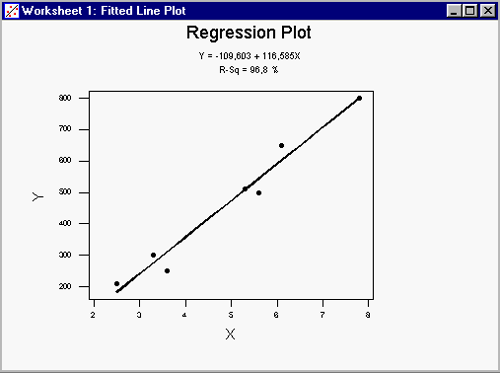
 | Observad que los diferentes puntos se encuentran bastante cerca de la recta de regresión. |
Apartado 4:
El error estándar de la pendiente se encuentra en la columna StDev y al lado del valor de la pendiente m (es decir, del coeficiente que acompaña la variable X):
Para encontrar el intervalo de confianza de la pendiente tenéis que aplicar la siguiente fórmula:
m ± tn-2,a/s.sm
donde n es el número de observaciones (en este caso, n = 7) i tn-2,a/s.sm es el valor crítico de la t de Student de n-2 grados de libertad que deja una probabilidad de a/2 a su derecha (recordad que si el nivel de confianza es del 95%, entonces el nivel de significación es a = 1 - 0,95).
Sustituyendo se obtiene el siguiente intervalo:
116,585 ± 2,5706 · 9,495
(92,177 ; 140,993)
Apartado 5:
Para ver si la pendiente es significativa, sólo hay que considerar el valor P asociado a este coeficiente. Si observáis el resultado de la regresión, el valor P vale 0,0000, lo que nos indica que es significativamente diferente de cero.
Apartado 6:
El valor de la varianza explicada para la recta de regresión se encuentra donde pone R-Sq, en este caso 0,968 (o equivalentemente, 96,8%). Observad que se trata de un valor situado entre 0 y 1. Dado que se encuentra muy cerca de 1 (el 96,8% de la variable Y viene explicada por la variable X), podemos decir que el ajuste es muy bueno.

