El ejemplo del apartado anterior consideraba una "variable de clasificación" o "variable explicativa" y una "variable de respuesta". El tratamiento formal que se hacía de éstas no era en ningún caso simétrico. Está claro, que un planteamiento inverso no tendría sentido, ya que no es posible un tratamiento simétrico de las dos variables: ¿podemos pensar que el hábito de fumar está relacionado con el sexo?

En muchas otras ocasiones conviene estudiar las relaciones entre variables análogas, sin que una de éstas se pueda ver como "respuesta" de otra.

Este análisis se realizará también con un test de ji cuadrado. En este caso se adoptará como hipótesis nula H₀: la independencia de las variables en la población considerada y para calcular las frecuencias esperadas con este enfoque se adopta un punto de vista probabilístico.

En este caso, si suponemos que hay independencia entre las variables (como corresponde a la hipótesis nula de ajuste al modelo que ahora interesa) resultará que la probabilidad de que un individuo de la muestra pertenezca a una casilla (fila f, columna c) debe ser igual a la "probabilidad" de pertenecer a la fila f multiplicado por la "probabilidad" de pertenecer a la columna c.

• Si representamos por T(f) el total de observaciones en la fila f; por T(c) el total de observaciones en la columna c y por N el número total de observaciones podemos escribir:

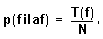
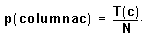
Entonces, bajo la hipótesis nula de independencia, la probabilidad p(f,c) de pertenecer a la casilla correspondiente a la fila f y la columna c se obtendrá multiplicando las dos anteriores y será:

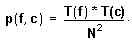
Por lo tanto, la frecuencia esperada en cada casilla, F_esp(f,c), que se obtendrá multiplicando la probabilidad de pertenecer a la casilla por el número total de datos observados, será, como en el caso del test de homogeneidad:

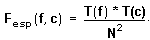
Observemos, pues, que a pesar de que el planteamiento inicial "teórico" ha sido diferente del que hemos realizado en el apartado anterior, las frecuencias esperadas son las mismas. Puesto que para calcular las frecuencias esperadas utilizamos los mismos totales (de datos, por filas y por columnas) que en el caso anterior, también coincidirá el número de grados de libertad con que hay que aplicar la prueba de ji cuadrado.

No habrá, pues, ninguna diferencia en la aplicación práctica del test. Lo que variará será el "comentario" que podremos hacer de acuerdo con las variables estudiadas y del papel que realicen unas respecto a las otras.

Acabaremos con un ejemplo didáctico (no le busquéis la finalidad estadística) de la aplicación de la prueba desde un punto de vista "manual". Puesto que no siempre se tiene el ordenador, también conviene conocer este procedimiento, que será diferente del que hay que adoptar cuando se trabaja con los programas informáticos.