El concepto de homogeneidad, de manera intuitiva, nos dice que no hay diferencia en la respuesta (segunda variable) respecto a los diferentes grupos en que se clasifica la primera variable.

¿Qué "aspecto" esperaríamos que tuviera una tabla cruzada que reflejase los valores aparejados de dos variables si presuponemos que hay homogeneidad en la respuesta?

Para calcular las frecuencias esperadas en cada casilla de una tabla cruzada, bajo la hipótesis de homogenenidad en la respuesta, se tomarán como datos los totales por filas y por columnas y se impondrá que, en cada fila, los porcentajes por filas sean iguales que los porcentajes de la fila de totales.

La tabla de frecuencias esperadas reproduce "la situación ideal", la proporcionada por la homogeneidad de la respuesta de una variable respecto a la otra en el conjunto de la población. El test de ji cuadrado servirá entonces para medir las discrepancias entre las frecuencias absolutas observadas en la muestra que se ha estudiado y las frecuencias esperadas bajo la hipótesis nula (que será de homogeneidad).

En el ejemplo que hemos presentado se partiría, pues, de los datos que hay en la tabla de la izquierda.

Se pueden calcular los porcentajes en la fila de totales: aptos (42,9%), no aptos (57,1%).

Para completar de tabla de frecuencias esperadas se impone que, en cada fila de la tabla "ideal" los porcentajes sean los que ya se han comentado. Así, por ejemplo, los hombres/aptos deberían ser el 42,9%.

A pesar de que las frecuencias esperadas, conceptualmente (por el hecho de que son frecuencias absolutas) deberían ser números enteros, en la aplicación del test de ji cuadrado se consideran con decimales si así resultan de la aplicación de la fórmula correspondiente.

Si se formula simbólicamente lo que se acaba de decir, resulta lo siguiente:

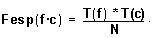
Ahora que ya tenemos criterios para decidir las frecuencias esperadas, podríamos aplicar una prueba de ji cuadrado..., pero nos falta comentar el número de grados de libertad que cabría considerar. Si, como sucede en este caso, a partir de las frecuencias observadas deducimos una serie de valores que después utilizamos para calcular las frecuencias esperadas, debemos rebajar los grados de libertad con que hay que aplicar el test.

En el ejemplo que nos ocupa se han utilizado los elementos siguientes:

• El número total de datos (que ya sabemos que siempre rebajan a 1 el número total de grados de libertad).
• Los totales de cada fila, pero de estos totales sólo son independientes tantos como filas haya menos 1 (porque la suma de todos estos totales es el número de observaciones).
• Los totales de cada columna, pero de estos totales sólo son independientes tantos como columnas haya menos 1 (porque la suma de todos estos totales es el número de observaciones).

Así, si indicamos como m el número de filas y como n, el número de columnas (sin contar las filas y columnas totales), el número de clases es m·n de las cuales hay que restar, por el total de datos, 1; por los totales de filas, m–1 y por los totales de columnas n–1, y obtendremos finalmente el número de grados de libertad con que hay que aplicar la prueba de ji cuadrado en el análisis de una tabla de doble entrada, que es: m·n – 1 – (m–1) (n–1) = (m–1)·(n–1).

Habitualmente, no nos tendremos que preocupar por los cálculos de la prueba del ji cuadrado, ya que nos los realizará el programa estadístico que utilizamos.

A causa de la extensión del tema, no trataremos aquí ni las pruebas de conformidad ni las de relación que son de uso tan frecuente.