


Riesgo de una cartera
Si la rentabilidad de una cartera no es más que la suma de las rentabilidades individuales de todos sus componentes ponderada por el peso de cada uno de ellos, el riesgo no sigue la misma dinámica en su composición; es decir, no es sólo la suma del riesgo de cada uno de los activos según su ponderación dentro de la cartera, sino que incluimos otro elemento en el análisis: la relación de la evolución entre las acciones. La formulación concreta es la siguiente:
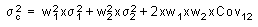
donde
| – | s2c | = | Riesgo de una cartera. |
| – | w1, w2 | = | Ponderación de cada acción en la cartera (según el capital invertido). |
| – | s21, s22 | = | Varianza del activo uno y dos respectivamente. |
| – | Cov12 | = | Covarianza entre las dos acciones. |
La covarianza nos indica la relación existente entre el comportamiento de las dos acciones. Concretamente, nos muestra cuál será la evolución de un activo al producirse una variación en el valor del otro.
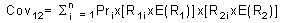
siendo
| – | Cov12 | = | Covarianza entre las dos acciones. |
| – | Pri | = | Probabilidad de que se produzca ese escenario. |

Si la covarianza es positiva, significa que cuando una acción sube la otra también lo hace. Si es negativa, quiere decir que cuando una sube la otra baja. Si la covarianza es prácticamente nula, significa que las dos acciones son independientes y el movimiento de una no afecta a la otra.
Aparte de la covarianza, también hay otro parámetro estadístico que nos indica la relación entre las dos acciones y que es más fácil de interpretar: el coeficiente de correlación (r12). La fórmula que lo identifica es la siguiente:
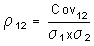
El coeficiente de correlación es un parámetro acotado entre 1 y –1 y su interpretación es simple. Si la acción 1 sube un 30% y la 2 desciende exactamente el mismo porcentaje, –30%, diremos que tienen una correlación negativa perfecta, y r12 = –1.

Si, por el contrario, al subir la 1 un 30% la acción 2 también lo hace en un 30%, tienen correlación positiva perfecta, con r12 = +1. Si r12 = 0, nos indica que la relación entre ambas acciones es nula.
Mediante la expresión del coeficiente de correlación podríamos aislar la covarianza, hecho que nos facilitaría el cálculo de la varianza de la cartera (el riesgo).
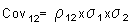
Con lo que la fórmula del riesgo de la cartera quedará:

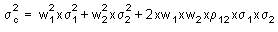
La anterior fórmula nos muestra que el riesgo de una cartera está constituido por el riesgo de cada una de las acciones más la relación que tengan los títulos entre sí. Este hecho es muy importante porque si el coeficiente de correlación (r12) entre las acciones es negativo, podríamos reducir el riesgo de la cartera apreciablemente, manteniendo el nivel de rentabilidad esperada.



