Como acabamos de decir, las jugadas estratégicas son interactivas, son decisiones de un jugador destinadas a afectar las creencias, las expectativas y, en definitiva, las acciones de los otros en un sentido favorable al que ha utilizado la jugada.

Recordemos ahora la matriz núm. 3, que representaba una estructura de recompensas distintas para Holmes y Moriarty según bajaran los dos en A, los dos en B o uno en A y el otro en B.

En relación con el juego representado por esta matriz núm. 3 habíamos presentado en el capítulo Conflicto y cooperación un experimento de negociación distributiva explícita (regateo) cuyo resultado básicamente consistía en que Moriarty compensaba a Holmes, en mayor o menor medida, para que éste se aviniera a bajar en A. Vimos también el abanico de resultados, tendentes mayoritariamente a la solución "justa" de 6-6. También habíamos observado -ante los resultados que nos proporcionaban poco después los experimentos de negociación tácita- que probablemente a Moriarty le convenía más no abrir negociaciones explícitas, ya que saldría mejor parado si hacía imposible la comunicación y bajaba en A. En efecto, en ausencia de toda posibilidad de comunicación, si Holmes actuaba racionalmente tendría que elegir también A.

Alterando momentáneamente las reglas del juego de turno simultáneo (recordemos, iban en trenes separados y no podían observar en qué estación bajaba el otro), supongamos ahora que uno de los dos jugadores, por ejemplo Moriarty, tiene la oportunidad de jugar primero y de que su jugada sea observada por Holmes. En otras palabras, pasemos de un juego de turno simultáneo a un juego de turno consecutivo. Obviamente, en tal caso, Moriarty bajaría en A (su mejor recompensa) y esperaría triunfalmente en el andén el paso del tren de Holmes quien, viendo por la ventanilla que Moriarty ya había bajado en A, sabría que su estructura de recompensas le planteaba ahora la sencilla disyuntiva de bajar él también en A y ganar 4, o bajar en B y no ganar nada. La posibilidad de que Holmes ganara 5 si bajaban ambos en B habría quedado excluida irreversiblemente por la previa jugada incondicional de Moriarty consistente en bajar en A. Por supuesto Holmes, que en nuestro juego es un agente económico racional, bajaría también en A y Moriarty habría obtenido su mejor resultado sin necesidad de pagar ninguna compensación, gracias simplemente a haber jugado primero.

	Jugar primero irreversiblemente y de forma que tal jugada irreversible sea observada por el otro jugador, cuando esto conviene a nuestros intereses, es una jugada estratégica porque induce el siguiente movimiento de nuestro oponente en el sentido que habíamos planeado.

Aunque intuitivamente ya parece clara la elección que ha de adoptar Moriarty si le permitimos jugar primero -y también cuál ha de ser la mejor respuesta de Holmes tras la jugada de su adversario-, podemos facilitar el análisis mediante el despliegue de un sencillo árbol de juego (o secuencia de decisiones en un juego de estrategia) representativo del itinerario de elecciones posibles para cada jugador en un juego de turno consecutivo y de las respectivas consecuencias de tales elecciones en orden a las recompensas. Si mantenemos la estructura de recompensas de la matriz núm. 3 pero permitimos a Moriarty jugar primero, el árbol de juego desde el punto de vista de Moriarty sería el siguiente:

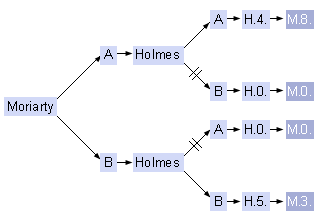
Un árbol de juego representa todos los posibles cursos de acción de un jugador confrontado a más de una elección y también todas las respuestas posibles del otro jugador a cada uno de las posibles elecciones del primero. Si sabemos cuáles van a ser tales respuestas (porque estamos actuando bajo condiciones de certeza –como es el caso del ejemplo precedente– o, al menos, bajo condiciones de alta probabilidad), podremos eliminar todos los cursos de acción (o ramas del árbol) que el otro jugador descartará (en este caso Holmes descartará siempre las opciones que le dan 0 puntos) y si podemos reconstruir todo el juego podremos evaluar cuál es la decisión actual que conduce a nuestro mejor resultado final. En nuestro ejemplo, si Moriarty elige A obtendrá al final un resultado de 8 y si elige B obtendrá al final un resultado de 3. En consecuencia, Moriarty debe elegir A.

De la misma forma, si ahora permitiéramos a Holmes jugar el primero el árbol de juego correspondiente a sus posibles cursos de acción sería el siguiente:

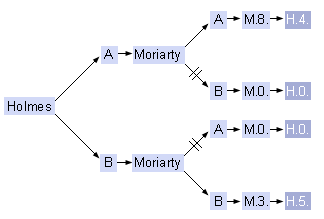
Por los mismos razonamientos expuestos más arriba, Holmes sabe que Moriarty descartará las opciones que le dan 0 puntos, por lo que se pueden eliminar tales cursos de acción de Moriarty (o ramas del árbol), y Holmes puede saber que si elige ahora A obtendrá al final 4 y si elige ahora B obtendrá al final 5. En consecuencia, debe elegir B.

Los árboles de juego que acabamos de ver ilustran también un principio básico de estrategia en los juegos de turno consecutivo, el que se formula como mirar hacia adelante y razonar hacia atrás y se denomina también principio de reconstrucción. Como señalan Dixit y Nalebuff...

	...tal principio consiste en prever las decisiones futuras de los demás jugadores y tomarlas en cuenta para adoptar nuestras decisiones actuales con el fin de evaluar cuál será nuestra mejor jugada.